Beam Deflection
In numerous cases of structural and machine
designs, members must repel the force applied indirectly or obliquely to their
axes. similar members are called shafts. The main members supporting the bottoms of
structures are shafts, just as an axle of an auto is a ray. numerous shafts act
contemporaneously as torsion members and as shafts. So far it can be said ray
is an integral part of the construction.
Beam Deflection
Beam deviation means the state of distortion
of a ray from its original shape under the work of a force or cargo or weight.
One of the most important operations of ray deviation is to gain equations with
which we can determine the accurate values of ray diversions in numerous
practical cases. diversions are also used in the analysis of statically
indeterminate shafts.
Styles to Determine Beam Deflection
Several styles are available for determining
ray diversions. The principle is the same but differs in fashion and in their
immediate ideal.
1.
Direct Integration system
2.
Area
Moment Method
3.
Conjugate
Beam Method
4.
system
of Superposition
Direct Integration Method
Beam diversions due to bending are determined
from distortion taking place along a span. This is grounded on the thesis that
during bending, aeroplane sections through a ray remain plain. For now, it'll be
assumed that bending takes place only at about one of the top axes of the
sampling. The edge view of the neutral face of a veered ray is called the
elastic wind of the ray. The discrimination equation of the elastic wind of a
ray
EId2ydx2=MEId2ydx2=M
The product EI is called the flexural
rigidity of the beam which is usually constant along the beam.
v = deflections of the elastic curve
θ = dv/dx = v' = slope
of the elastic curve
M=EId2vdx2=EIv′′M=EId2vdx2=EIv′′
V=dMdx=ddx(EId2vdx2)=(EIv′′)′V=dMdx=ddx(EId2vdx2)=(EIv′′)′
q=dVdx=d2dx2(EId2vdx2)=(EIv′′)′′q=dVdx=d2dx2(EId2vdx2)=(EIv′′)′′
By simplifying-
EId2vdx2=M(x)EId2vdx2=M(x)
EId3vdx3=V(x)EId3vdx3=V(x)
EId4vdx4=q(x)EId4vdx4=q(x)
Here q(x) is the load function. The
choice of which equation we will use to determine v depends on the ease with
which an expression for moment, shear or load can be formulated.
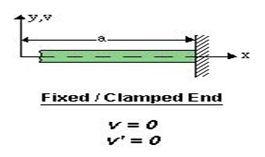
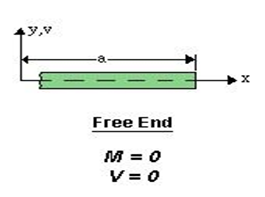
Some Boundary Conditions:
- Clamped or fixed support:
- Roller or pinned support:
In this case. the end is free to rotate, that’s why the moment is zero.
- Free end:
- Guided Support:
Er. SP. ASWINPALANIAPPAN.,
M.E., (Strut/.,)., (Ph.D.,)
Structural Engineer


No comments:
Post a Comment