Isolated footing design as per IS 456-2000 code | structural design | civil engineering
Footing the structure which exists below the ground level; the strength of the building is depending upon the reinforcement details of the foundation. The reinforcement details depend upon the total load which is acts on building structures. The loads related to the gravity loads and gravity loads are considered in the foundation design. The load is taken as a point load which acts in the column section. In this article, I will explain to you the clear concept regarding the isolated footing design as per IS 456-2000 code by manual calculations. In the column design and assume the load is taken as 1200kN and dimensions of the columns are obtained as 400mmX400mm cross-section.
Basic formulas used in the design as per IS456-2000 code
For the design of RCC footing as per the IS456 code the following 8 basic formulas are used which are given as per IS 456 standards.
- Area of footing = Total load/SBC
- Soil pressure = qu = Total load/Area of footing
- Factored shear force Vu1 = (quB/2) (B-C1-2d)
- One way shear resistance = Vc1 = τcbd
- Factored shear force / Two way shear = Vu2 = qu (B2-(C1+d)2)
- Punching / Two-way shear resistance = Vc2 =Ksτcb0d
- Ultimate moment Mu = (quB/8) (B-C)2
- Mu = 0.87fyAstd(1-(Astfy/bdfck))
Steps used in Isolated footing design as per IS 456 code
The following six steps are used in the isolated footing design as per IS 456
- Load calculations
- Size of footings
- Calculation of net upward pressure at ultimate load
- Calculation of one-way shear to determine the depth
- Check for punching shear / Two-way shear
- Reinforcement design
Example of Isolated footing design as per IS 456-2000 code standards
Design RCC isolated footing for 400 mmX400 mm column size which carries a load of 1200kN on the column, take Soil bearing capacity of the soil (SBC) is 200kN/m2. Assume M20 grade concrete and Fe 415 grade steel.
Step 1: Load calculations
Given load P = 1200kN
Factor load (or) ultimate load = 1.5P = 1.5X1200 = 1800kN
Consider self-weight of footing and backfill is 10% column load
= (10%column load) = (10/100)1800 = 120kN
Now the total load on the column = Factor load + 10% column load
= 1800+120 =1920 kN
Step 2: Size of footings calculations
As per step1, the total load is obtained as 1920 kN
Let us consider the square footing which is having length and width as B
So the area of footing is given by BXB = B2
As per the formula of area of footing is given by
B2 = Total load/SBC = 1920/200 = 9.6 m2
By solving we can get the value of B = 3.1m
So final area of footing provided is = 3.1mX3.1m =9.61 m2
Step 3: Calculation of net upward pressure at ultimate load
The calculated ultimate load from step 1 is 1920kN
Soil pressure = qu = Total load/Area of footing = 1920/9.61 = 199.80 kN/m2
So take soil pressure qu = 200 kN/m2
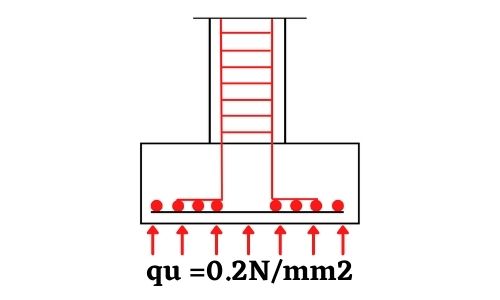
Step 4: Calculation and check for one way shear to determine the depth
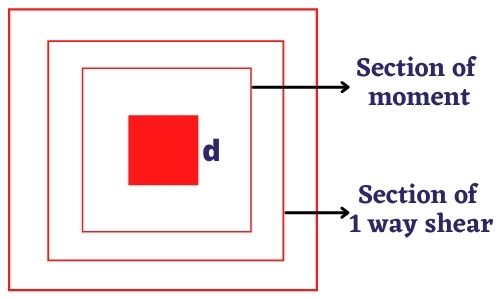
From formulae of factored shear force for one-way shear
Factored shear force Vu1 = (quB/2) (B-C1-2d)
By taking the values Vu1 = ((0.2X3100)/2)(3100-400-2d)
By solving the above equation we can get
Vu1 = 310(2700-2d) ————————– equation 1
By assuming the percentage of steel in the footing
Pt =0.15%
From table 19 of IS 456-2000 code
Design shear = 0.36 N/mm2
And one way shear resistance is given by Vc1 = τcbd
By substituting the values Vc1 = 0.36X3100d
Vc1 =1116d ——————————- equation 2
By solving equation 1 and equation 2
310(2700-2d) = 1116d
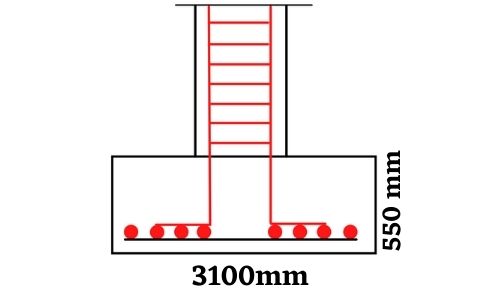
We can get the value of d as 482.19mm
Let us consider the cover as 68mm
So overall depth is given by 482+68 = 550mm
Step 5: Check for punching shear / Two-way shear
Since we have formulae
Factored shear force / Two way shear = Vu2 = qu (B2-(C1+d)2)
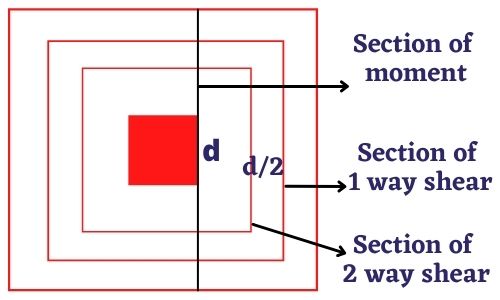
By substituting the values in the above expression
Vu2 = 0.2 (31002 – (400+550)2)
= 1741.5 kN
Again we have punching / two-way shear resistance
Vc2 = Ksb0d
Where b0 = 4(C1+d)
= 4(400+550)
= 3800
From clause 31.6.3 permissible shear stress ( IS 456-2000)
c = 0.25 fy1/2 = 0.25X201/2 = 1.118 N/mm2 and Ks =1
By substituting the values we can get
Vc2 = 1X1.118X3800X550
= 2336.62 kN
So here Vc2 > Vu2, hence 550mm depth is safe
Step 6: Reinforcement design calculation
We have the ultimate moment expression from the formulae section
Mu = (quB/8) (B-C)2
By substituting the values we can get
Mu = ((0.2X3100)/8) (3100-400)2
Mu = 564.975 kN.m
By using the Mu expression we can easily calculate the Ast value
Mu = 0.87fyAstd(1-(Astfy/bdfck))
564.975 X 106 = 0.87X20XAstX550 (1-(AstX415/3100X400X20))
By solving the above equation we can get the value of Ast
So here Ast = 2951.4 mm2
Let us consider 16mm diameter bars
Area of 1 bar provided = µ/4(16)2 = 201 mm2
Number of bars required = Ast/Area of 1 bar = 2951.4/201 = 14.68no’s
Take 15 numbers of 16 mm diameter bars
Spacing = (A/Ast)XB
= (201/2951.4)X3100
= 211.12 mm
So the final reinforcement for isolated footing as per IS 456-2000 code is obtained by using 16mm diameter bars at 210 C/C distance in both X direction and Y direction.
The final reinforcement view is shown in the below figure.
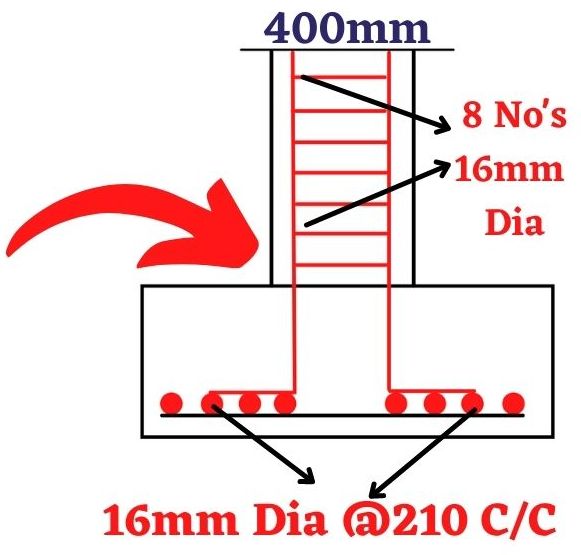
Conclusion of complete isolated footing design as per IS 456-2000 code
Well, now the above-explained concepts are related to the complete design of isolated footing as per IS 456-2000 code. The detailed calculation is shown for a 1200kN load with a column size of 400mmX400mm dimensions. As per the final detailing the reinforcement details are obtained by using 16mm diameter bars at 210 C/C distance in both the X direction and Y direction.
Er. SP. ASWINPALANIAPPAN., M.E., (Strut/.,)., (Ph.D.,)
Structural Engineer