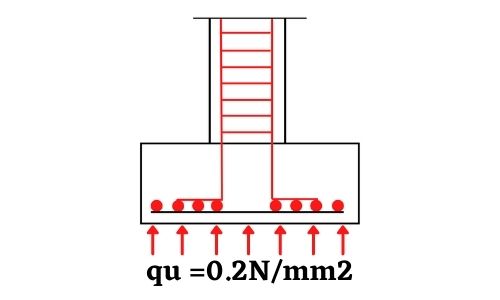
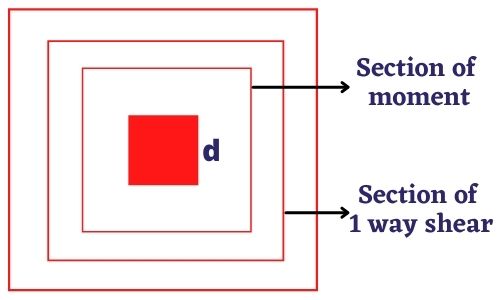
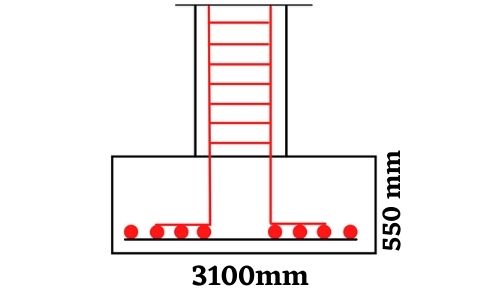
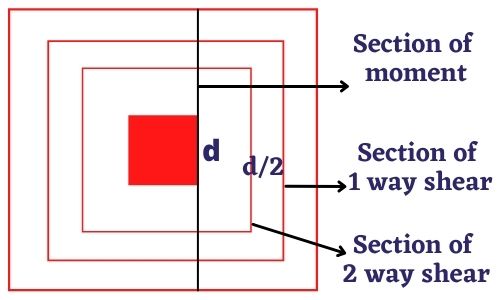
INTRODUCTION
Thermal bridging occurs when a relatively small
area of a wall, floor, or roof loses much more heat than the surrounding area.
Thermal bridging can occur in any type of building construction. The effects of
thermal bridging may include increased heat loss, occupant discomfort,
unanticipated expansion/contraction, condensation, freeze-thaw damage, and
related moisture and/or mold problems for materials susceptible to moisture.
The severity of the thermal bridge is determined by the extent of these
effects.
Thermal bridges, and the subsequent damage, can be
avoided by several strategies which are best implemented during the design stage
when changes can be easily incorporated. After construction, repairing thermal
bridges can be both costly and difficult.
THERMAL BRIDGING
A thermal bridge allows heat to “short circuit”
insulation. Typically, this occurs when a material of high thermal
conductivity, such as steel framing or concrete, penetrates or interrupts a
layer of low thermal conductivity material, such as insulation. Thermal bridges
can also occur where building elements are joined, such as exposed concrete
floor slabs and beams that abut or penetrate the exterior walls of a building.
Causes
Thermal bridging is most often caused by improper
installation or by material choice/building design. An example of improper
installation leading to thermal bridging is gaps in insulation, which allow
heat to escape around the insulation and may also allow air leakage. For this
reason, insulation materials should be installed without gaps at the floor,
ceiling, roof, walls, framing, or between the adjacent
insulation materials. Further, insulation materials should be installed so
that they remain in position over time.
Although thermal bridging is primarily associated
with conduction heat transfer (heat flow through solid materials), thermal
bridging effects can be magnified by heat and moisture transfer due to air
movement, particularly when warm, moist air enters the wall. For this reason,
buildings with typically high interior humidity levels, such as swimming pools,
spas, and cold storage facilities, are particularly susceptible to moisture
damage. Proper installation of vapor and air retarders can greatly reduce
moisture damage caused by thermal bridges. Concrete masonry construction does
not necessarily require separate vapor or air retarders: check local building
codes for requirements.
Minimizing moisture leakage will also alleviate
thermal bridging due to air leakage for two reasons: air will flow through the
same points that allow moisture entry; and water leakage can lead, in some
cases, to degradation of air barriers and insulation materials.
Effects
Possible effects of thermal bridges are:
- increased heat loss through the wall, leading to higher operating
costs,
- unanticipated expansion and/or contraction,
- local cold or hot spots on the interior at the thermal bridge
locations, leading to occupant discomfort and, in some cases, to
condensation, moisture-related building damage, and health and safety
issues,
- local cold or hot spots within the wall construction, leading to
moisture condensation within the wall, and possibly to damage of the
building materials and/or health and safety problems, and/or
- local warm spots on the building exterior, potentially leading to freeze-that
damage, such as ice dams, unanticipated expansion or contraction, and
possible health and safety issues.
Not all thermal bridges cause these severe effects.
However, the severity of a particular thermal bridge should be judged by the
effect of the thermal bridge on the overall energy performance of the building;
the effect on occupant comfort; the impact on moisture condensation and
associated aesthetic and/ or structural damage; and degradation of the building
materials. Appropriate corrective measures can then be applied to the design.
Requirements
ASHRAE Standard 90.1, Energy Standard for Buildings
Except for Low-Rise Residential Buildings (ref. 1) (included by reference in
the International Energy Conservation Code (ref. 2)) addresses thermal bridging
in a wall, floor, and roof assemblies by mandating that thermal bridging be
accounted for when determining or reporting assembly R-values and U- factors.
For concrete masonry walls, acceptable methods for determining
R-values/U-factors that account for the thermal bridging through concrete
masonry unit webs include testing, isothermal planes calculation method (also
called series-parallel calculation method), or two-dimensional calculation
method. NCMA-published R-values and U-factors, such as those in TEK 6-1C, R-Values of Multi-Wythe Concrete Masonry
Walls, TEK 6-2C, R-Values and U-Factors for Single Wythe Concrete
Masonry Walls, and the Thermal Catalog of Concrete Masonry Assemblies (refs.
4, 5, 6), are determined using the isothermal planes calculation method. The
method is briefly described in TEK 6-1C as it applies to concrete masonry walls.
SINGLE WYTHE MASONRY WALL
In a single wythe concrete masonry wall the webs of
the block and grouted cores can act as thermal bridges, particularly when the
cores of the concrete masonry units are insulated. However, this heat loss is
rarely severe enough to cause moisture condensation on the masonry surface or
other aesthetic or structural damage. These thermal bridges are considered when
determining the wall’s overall R-value, as noted above. In severe climates, in
certain interior environments where condensation may occur under some conditions,
or when otherwise required, the thermal bridging effects can be eliminated by
applying insulation on the exterior or interior of the masonry, rather than in
the cores. In addition, thermal bridging through webs can be reduced by using a
lighter-weight masonry unit, by using special units with the reduced web site,
or by using units that have fewer cross webs.
Horizontal joint reinforcement is often used to
control shrinkage cracking in concrete masonry. Calculations have shown that
the effect of the joint reinforcement on the overall R-value of the masonry
wall is on the order of 1 – 3%, which has a negligible impact on the building’s
energy use.
CONCRETE MASONRY CAVITY WALL
In masonry cavity walls, insulation is typically
placed between the two wythes of masonry, as shown in Figure 1. This provides a
continuous layer of insulation, which minimizes the effects of thermal bridging
(note that some references term the space between furring or studs as a
“cavity,” which differs from a masonry cavity wall).
Because the wall ties are isolated from the
interior, the interior surface of the wall remains at a temperature close to
the building’s interior temperature. The interior finish material is not likely
to be damaged due to moisture condensation, and occupant comfort is not likely
to be affected. As with horizontal joint reinforcement in single wythe
construction, the type, size, and spacing of the ties will affect the potential
impact on energy use.

Figure
1—Insulated Masonry Cavity Wall
MASONRY VENEER WITH STEEL STUD BACKUP
Figure 2 shows a cross section of a typical
concrete masonry veneer over a steel stud backup. Steel studs act as strong
thermal bridges in an insulated wall system. Almost 1,000 times more heat flows
through the steel than through mineral fibre insulation of the same thickness
and area. The steel stud allows heat to bypass the insulation and greatly
reduces the insulation’s effectiveness.
Just as for concrete masonry webs, the thermal
bridging through steel studs must be accounted for. According to ASHRAE
Standard 90.1, acceptable methods to determine the R-value of insulated steel
studs are testing, modified zone calculation method, or using the
insulation/framing layer adjustment factors shown in Table 1. The effective
framing/cavity R-value shown in Table 1 is the R-value of the insulated steel
stud section, accounting for thermal bridging. Using these corrected R-values
allows the designer to adequately account for the increased energy use due to
the thermal bridging in these wall assemblies.
Table 1 shows that thermal bridging through steel
studs effectively reduces the effective R-value of the insulation by 40 to 69
percent, depending on the size and spacing of the steel studs and on the
R-value of the insulation.
Because the steel studs are typically in contact
with the interior finish, local cold spots can develop at the stud locations.
In some cases, moisture condenses causing dampness along these strips. The damp
areas tend to retain dirt and dust, causing darker vertical lines on the
interior at the steel stud locations. If warm, moist indoor air penetrates the
wall, moisture is likely to condense on the outer flanges of the steel studs,
increasing the potential for corrosion of studs and connectors and structural
damage to the wall. Gypsum sheathing on the exterior of the studs can also be
damaged due to moisture, particularly during freeze-thaw cycles. These impacts
can be minimized by including a continuous layer of insulation over the steel
stud/insulation layer.

Figure
2—Concrete Masonry Veneer with Steel Stud Backup

Table
1—Effective Insulation/Framing Layer R-Values for Wall Insulation Installed
Between Steel Framing (ref. 1)
SLAB EDGE & PERIMETER BEAM
Another common thermal bridge is shown in Figure 3.
When this wall system is insulated on the interior, as shown on the left,
thermal bridging occurs at the steel beam and where the concrete floor slab
penetrates the interior masonry wythe.
A better alternative is to place insulation in the
cavity, as shown on the right in Figure 3, rather than on the interior. This
strategy effectively isolates both the slab edge and the steel beam from the
exterior, substantially reducing heat flow through these areas and condensation
potential and decreasing heating loads (ref. 3).
A third alternative, not illustrated, is to install
insulation on the interior of the steel beam. This solution, however, does
not address the thermal loss through the slab edge. In addition, the interior
insulation causes the temperature of the steel beam to be lower and can lead to
condensation unless a tight and continuous vapor retarder is provided.

Figure
3—Alternative Insulation Strategies for Slab Edge and Perimeter Beam
MASONRY PARAPET
Because a parapet is exposed to the outside
environment on both sides, it can act as a thermal fin, wicking heat up through
the wall. Figure 4 shows two alternative insulation strategies for a masonry
parapet. On the left, even though the slab edge is insulated, the parapet
is not. This allows heat loss between the roof slab and the masonry backup.
A better alternative is shown on the right in
Figure 4. Here, the parapet itself is insulated, maintaining a
thermal boundary between the interior of the building and the outdoor
environment. This significantly reduces heating and cooling loads, and
virtually eliminates the potential for condensation on the underside of the
roof slab.

Figure
4—Alternative Insulation Strategies for a Masonry Parapet
References
1. Energy Standard for
Buildings Except for Low-Rise Residential Buildings ASHRAE Standard 90.1. American
Society of Heating, Refrigerating, and Air-Conditioning Engineers, 2004 and
2007.
2. International Energy
Conservation Code. International Code Council, 2006 and 2009.
3. ASHRAE Handbook—HVAC
Applications. American Society of Heating, Refrigerating, and Air-Conditioning Engineers,
2007.
4. R-Values of Multi-Wythe
Concrete Masonry Walls, TEK 6-1C. National Concrete Masonry Association, 2013.
5. R-Values and U-Factors for
Single Wythe Concrete Masonry Walls, TEK 6-2C. National Concrete Masonry Association, 2013.
6. Thermal Catalog of
Concrete Masonry Assemblies, TR233. National Concrete Masonry Association, 2010.
NCMA TEK 6-13B, Revised 2010.
NCMA and the companies disseminating this technical
information disclaim all responsibility and liability for the accuracy and application
of the information contained in this publication.
Thanks to
NCMA
Er. SP. ASWINPALANIAPPAN., M.E., (Strut/.,)., (Ph.D.,)
Structural Engineer
http://civilbaselife.blogspot.com